Hello coders, welcome to codingbroz !!! Today in this article we will talk about What are graphs? What are the types of graphs? What are the terminologies used for graphs? and all about Basics of Graph Data Structure
What is a Graph Data Structure ?
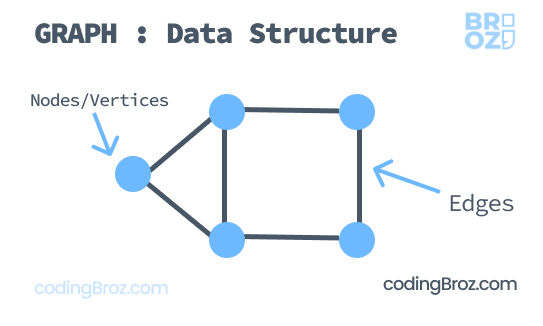
Graph is a non-linear data structure. It mainly consists of 2 components – nodes(or vertices) and edges(or arcs) .
Definition of Graph :
Graph is a collection of nodes and edges, where nodes are connected with edges.
OR
Graph is a collection of vertices and arcs, where vertices are connected with arcs.
Now, a Graph G can be represented as G = (V,E), where V is a set of vertices and E is a set of edges.
Example of Graph :
This is a graph with 5 vertices and 6 edges.
This graph G can be defined as G = ( V , E )
Where V = {A,B,C,D,E} and E = {(A,B),(A,C)(A,D),(B,D),(C,D),(B,E),(E,D)}.
Types of Graphs :
There are two types of graphs :
- Undirected graphs
- Directed graphs
What is an undirected graph ?
In an undirected graph , the edges are not associated with any directions. If an edge exists between vertex A and B then the vertices can be traversed from B to A as well as A to B.
What is a directed graph ?
In an undirected graph , the edges are associated with directions. If an edge exists between vertex A and B then the vertices can be traversed only from A to B and not from B to A.
Some Graph Terminologies :
These are the some important terms used for graph data structure –
Vertex
Individual data element of a graph is called a Vertex. Vertex is also known as node. In the above example graph, A, B, C, D & E are known as vertices.
Edge
An edge is a connecting link between two vertices. Edge is also known as Arc. An edge is represented as (startingVertex, endingVertex). For example, in the above graph the link between vertices A and B is represented as (A,B). In the above example graph, there are 7 edges (i.e., (A,B), (A,C), (A,D), (B,D), (B,E), (C,D), (D,E)).
Edges are three types.
- Undirected Edge – An undirected edge is a bidirectional edge. If there is an undirected edge between vertices A and B then edge (A , B) is equal to edge (B , A).
- Directed Edge – A directed edge is a unidirectional edge. If there is a directed edge between vertices A and B then edge (A , B) is not equal to edge (B , A).
- Weighted Edge – A weighted edge is an edge with value (cost) on it.
Undirected Graph
A graph with only undirected edges is said to be an undirected graph.
Directed Graph
A graph with only directed edges is said to be a directed graph.
Mixed Graph
A graph with both undirected and directed edges is said to be a mixed graph.
End vertices or Endpoints
The two vertices joined by an edge are called end vertices (or endpoints) of that edge.
Origin
If an edge is directed, its first endpoint is said to be the origin of it.
Destination
If an edge is directed, its first endpoint is said to be the origin of it and the other endpoint is said to be the destination of that edge.
Adjacent
If there is an edge between vertices A and B then both A and B are said to be adjacent. In other words, vertices A and B are said to be adjacent if there is an edge between them.
Incident
Edge is said to be incident on a vertex if the vertex is one of the endpoints of that edge.
Degree
Total number of edges connected to a vertex is said to be the degree of that vertex.
Indegree
Total number of incoming edges connected to a vertex is said to be indegree of that vertex.
Outdegree
Total number of outgoing edges connected to a vertex is said to be outdegree of that vertex.
Parallel edges or Multiple edges
If there are two undirected edges with same end vertices and two directed edges with same origin and destination, such edges are called parallel edges or multiple edges.
Self-loop
Edge (undirected or directed) is a self-loop if its two endpoints coincide with each other.
Simple Graph
A graph is said to be simple if there are no parallel and self-loop edges.
Path
A path is a sequence of alternate vertices and edges that starts at a vertex and ends at another vertex such that each edge is incident to its predecessor and successor vertex.
Conclusion
Today, you learned what is a graph data structure? and some important graph terminologies.
Hope you found our article helpful !!! Go checkout some other resources and articles as well on codingbroz 🙂